GA 2D Simulator
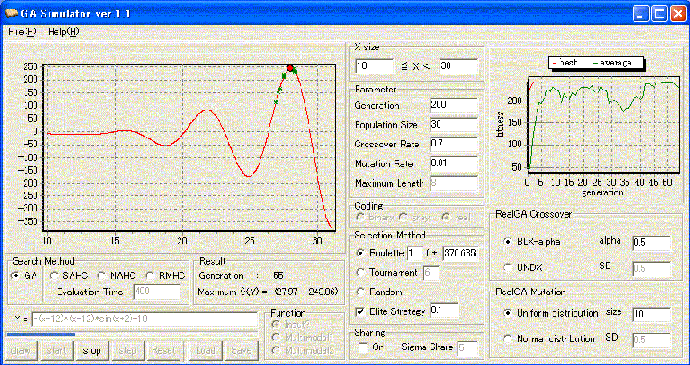
GA 2D Simulatorとは遺伝的アルゴリズムを楽しく学んじゃおうというソフトです。その概観は以下のとおりです。 遺伝的アルゴリズムや山登り法といった手法を駆使してグラフの最高点を求めます。このソフトは2次元ですが3次元のバージョンもあります。
ダウンロード
GA 2D Simulator ver1.1 (410KB)
このファイルをダウンロードし解凍すると「EquToDbl.dll」と「EquToDbl.txt」と「GA2DSimulator.exe」という3つのファイルが出てきます。そして「GA2DSimulator.exe」をクリックするとGA
2D Simulatorを起動することができます。なおこのシミュレータにはやす兵衛さんが作られた数式計算DLLを利用させていただいています。
GA 2D Simulatorの使い方
GA 2D Simulatorの遊び方は簡単です。わからないところがあればこの使い方の説明のあとにある各機能の説明についても読んでみてください。
- Drawボタン もしくは Loadボタン
Drawボタン押すとGAでは初期世代が、山登り法ではランダムに作られた個体が表示されます。Loadボタンを押すと以前に保存された遺伝子データが書かれたテキストファイルを読み込むことができます。もちろんそのテキストファイルを書き換えて自分好み(?)の遺伝子を作ることもできます。ただしそのときは遺伝子長とかに気をつけてください。
- Startボタン
これを押すと計算を始めます。
- Stopボタン
これを押すと計算を中断することができます。途中の個体の動きをじっくり見たいときとかに使ってください。
- Stepボタン
Stopボタンを押したあとStepボタンは使えるようになります。StepボタンはGAでは世代ごと、山登り法では評価回数ごとの動きを逐次見ることができます。
- Saveボタン
これを押すとその世代、または評価回数のときの個体の遺伝子を保存することができます。GAの場合はGA_DATA.txtというファイルに、山登り法のときはHC_DATA.txtというファイルの中に書き込まれます。
- Resetボタン
計算が終わったらこれを押してください。もう一度始めることができます。
Serch Method
探索手法のパラメータを設定します.
- Learning rate
PBILにおける学習パラメータです. - Truncation selection size
この適応度より大きい個体を選択します. - Crossover
交叉方法です.「One-point(一点交叉)」と「Uniform(一様交叉)」のどちらかを選択します. - Elite Rate
エリート戦略により残す個体の割合です. - Crossover Rate
交叉率です. - Mutation Rate
突然変異率です. - Selection
選択方法です.「Tournament」,「Roulet」,「Random」のいずれかを選択します.
ここではGA、SAHC、NAHC、RMHCの四つの手法を選ぶことができます。以下にその各手法の説明をします。
- GA(Genetic Algorithm)--遺伝的アルゴリズム--
遺伝的アルゴリズムとは、最適化を高速に行うための探索アルゴリズムの一種であります。GAは生物の進化、例えば選択、交叉突然変異といったものにヒントを得た比較的単純な手順を有し、ほとんどあらゆる最適化、探索の問題に適用可能な方法であります。GAでは遺伝子をもつ仮想的な生物の集団を計算機内に設定しあらかじめ定めた環境に適応している個体が、子孫を残す確率が高くなるよう世代交代シミュレーションを実行し遺伝子および生物集団を"進化"させます。
- SAHC(Steepest-ascent hill climbing)--最急勾配山登り法--
- まず1つの遺伝子配列を選びます。そしてこれを「現頂上」を呼ぶこととします。
- この遺伝子配列を左から右に順に1ビットずつ反転させて、それぞれの適合度を記録します。
- もし反転した結果適合度が増加するなら現頂上を反転結果の中で最も優れた適合度の遺伝子配列に変更します。
- もし適合度の増加がない場合は現頂上を保存し1に戻ります。そうでなければ2に移動します。
- 設定した回数の関数評価が済んだならば見つかった最高の頂上を答えとして出力します。
- NAHC(Next-ascent hill climbing)--逐次勾配山登り法--
- まず1つの遺伝子配列を選びます。そしてこれを「現頂上」を呼ぶこととします。
- SAHCと同様にビットを順順に変えていって適合度の増加が見られたら他の反転結果を見ることなく、それを現頂上とします。そしてこれを繰り返します。ただし反転するビット位置は先に適合度の見られたビット位置の隣から始めます。
- もし適合度の増加が見られない場合は現頂上を保存して1に戻ります。
- 設定した回数の関数評価が済んだならば見つかった最高の頂上を答えとして出力します。
- RAHC(Random-ascent hill climbing)--ランダム勾配山登り法--
- まず1つの遺伝子配列を選びます。そしてこれを「最高評価解」を呼ぶこととします。
- この遺伝子配列からランダムに1ビット反転させて、現在の適合度より優れた結果が得られるならそれを最高評価解とします。
- 最適な遺伝子が見つかるか定められた回数の関数評価が済むまで2に戻り繰り返します。
- もし適合度の増加が見られない場合は現頂上を保存して1に戻ります。
- 設定した回数の関数評価が済んだならば見つかった最高の頂上を答えとして出力します。
X_SIZE
グラフの最高値を求めるためにX座標に範囲を設けます。
Parameter
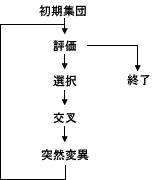
- Generation
世代数です。GAの時だけ利用します。世代とは右図のような一連の処理のことを言います。
- Population Size
集団サイズのことです。山登り法のときは最初の遺伝子がこれらの中からランダムに1つ選び出されます。GAのときはこれを基準として世代を繰り返していきます。
- Crossover Rate
交叉率のことです。GAのときだけ使います。交叉とはランダムに遺伝子座を選択し、子孫を生成するために2つの染色体間で遺伝子座の前と後を交換します。例えば、10000100と11111111の2つの染色体が3番目の遺伝子座で交叉された場合、これらから得られる子孫は10011111と11100100となります。交叉操作は2つの単一染色体生物間の生殖を単純化して模倣しています。
- Mutation Rate
突然変異率です。これもGAの時だけ使います。この操作は染色体中のビットのいくつかをランダムに反転させることです。
- Maximum Length
これは遺伝子長を表しています。GAのときも山登り法のときにも関係してきます。
Coding
固定長で0と1を用いて遺伝子を表す方法と、実数で表す方法があります。0と1での表し方にもいろいろありますが今回は以下のバイナリ・コーディングとグレイ・コーディングの2種類を使用しています。実数の方は、GAの場合のみで有効です。
- binary
もっとも一般的なコーディング方法です。xの範囲が10から30までで遺伝子長が8ビットの場合00000000がx=10を11111111がx=30を表すように01のビットを並べます。それを各個体の遺伝子とします。
- gray
GAで問題を効率よく処理するにはコーディングも重要な要素となります。バイナリコーディングの場合10進表記で隣り合っている値のハミング距離が1にならない部分があります。例えば2進表記で3は011となるのに4は100となっています。このようになっている場合3が最高値で4がその次に評価が高いとするとGAで生まれた子供は親に比較的に通っているのでほどほど高い4の周辺に集まってしまったとき3を見つけにくくなってしまいます。このような問題を解消するのがグレイ・コーディングです。グレイ・コーディングを行うと隣り合う数字のハミング距離は1になります。グレイ・コーディングの求め方を以下に示します。
- 2進数⇒Gray
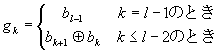
- Gray⇒2進数
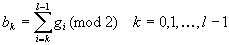
ちなみに10進数、2進数、Grayコードを比較してみると以下のようになります。
|
10進数 ---------- 0 1 2 3 4 5 6 7 |
2進数 ---------- 000 001 010 011 100 101 110 111 |
Grayコード ---------- 000 001 011 010 110 111 101 100 |
- real
実数を用いたコーディング方法です。この場合、交叉や突然変異を行うには上記の2種類とは異なる方法が必要です。詳しくはRealGA CrossoverとRealGA Mutationの項を見てください。
Selection Method
- Roulette
ルーレット方式とは適合度に比例した割合で選択する方法です。これは適合度に比例した領域を持つルーレットによるものであります。これは適合度に比例した領域をもつルーレットを回し、ルーレットの玉が入った領域の個体を選び出すというものであります。例えば
| f1 1.0 |
| f2 2.0 |
| f3 0.5 |
| f4 3.0 |
| f5 3.5 |
という場合を考えと、このとき重み付けのルーレットでの選択を次のように実現します。
f1+f2+f3+f4+f5=10.0
であるので0から10までの乱数を一様に発生させると、そして次の規則に従って選択します。
| 乱数の値が0.0〜1.0 ⇒ f1の個体を選択する。 |
| 乱数の値が1.0〜3.0 ⇒ f2の個体を選択する。 |
| 乱数の値が3.0〜3.5 ⇒ f3の個体を選択する。 |
| 乱数の値が3.5〜6.5 ⇒ f4の個体を選択する。 |
| 乱数の値が6.5〜10.0 ⇒ f5の個体を選択する。 |
今回このシミュレータでは適合値がマイナスになる可能性もあるので線形スケーリングを用いて補正を行っています。f'=af+bという式を用いて適合度にマイナスが出ないようにしました。デフォルトではaに1、bに設定されている範囲の関数の最小値を代入するようにしています。
- Tournament
これは集団の中からある個体数(=S、これは各自で好きなように決められます)をランダムに選び出してその中で一番良いものを選択することです。この過程を集団数が得られるまで繰り返すというものです。先の例を再び用いると
| f1 1.0 |
| f2 2.0 |
| f3 0.5 |
| f4 3.0 |
| f5 3.5 |
Sとして例えば3が採用された場合、このとき5回のトーナメントで選ばれた個体がおのおの次のようになったとすると
| 1回目のトーナメント f1,f2,f3 |
| 2回目のトーナメント f3,f4,f1 |
| 3回目のトーナメント f1,f5,f2 |
| 4回目のトーナメント f2,f4,f1 |
| 5回目のトーナメント f5,f2,f4 |
このとき各トーナメントの勝者はおのおの、f2、f4、f5、f4、f5となり、これらの個体が選択されます。この方式はトーナメントサイズSの値で様々なバリエーションがあります。
- Random
ランダム選択では交叉と対象となる遺伝子をランダムに選びます。なのであまり優れた結果はでないはずです。特にエリート戦略をしないとその特徴は顕著にわかるでしょう。
- Elite Strategy
ここにチックを入れるとエリート戦略が行われます。エリート戦略とは多くの選択方法に付加的なもので各世代における最良個体を強制的に保持させるものです。エリート戦略がGAの性能を大きく改善することはすでに確認されています。実際にこのシミュレーターでも目に見えてその違いがわかるでしょう。
Sharing
- Sharing
ここにチェックをいれると割り当て関数(Sharing function)を利用します。割り当て関数とは
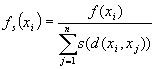
という式であります。d(x,y)というのは個体間のハミング距離であり、s(d)というのは下の図のような関数であります。これを使うと、多くの個体が同じ近傍にいるときには割り当ての総数が増えて適合度が低くなります。結果として、集団内での特定の種だけの増長を制限していることになります。実数値GAの場合、ハミング距離ではなく2数の距離を用いています。
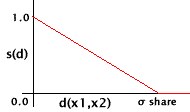
- Sigma Share
シグマ・シェアとは上のグラフからもわかるように、01によるコーディングの場合は各個体間のハミング距離のことです。例えば001と011との距離の差は2となります。
Function
- Input?
これにチェックを入れると自由に関数を定義することができます。変数は小文字の x です。大文字の X は使えません。他に使える関数は以下のとおりです。
| [定数] |
数値 pi deg e g T0 P0 |
数値定数(1, 2.0, 3.0E10 等) 円周率(3.1416...) pi / 180 自然対数の底(2.7182....) 重力加速度(9.80665) 絶対温度(273.15) 大気圧(101325) |
| [演算子] |
- + - * / ^ ! |
負の数値 四則演算 ベキ乗 階乗 |
| [関数] |
abs(x) |x| sqrt(x) exp(x) log(x) log10(x) sin(x) cos(x) tan(x) asin(x) acos(x) atan(x) sinh(x) cosh(x) tanh(x) |
絶対値 絶対値 平方根 指数 自然対数 常用対数 サイン コサイン タンジェント 逆サイン 逆コサイン 逆タンジェント ハイパボリックサイン ハイパボリックコサイン ハイパボリックタンジェント |
- Multimodal1
これにチェックを入れると y=|sin(x)| の関数が表示されます。これはシェアリングの効果を確かめるために利用することができます。
- Maltimodal2
これにチェックを入れると y=x×|sin(x)| の関数が表示されます。これもシェアリングの効果を確かめるために利用することができます。
RealGA Crossover
この項目は、Real GAのときのみ作用します。
- BLX-α
この交叉法は、次のように子を決めます。
- 2つの親個体をa,bとします。
- 子個体を区間[A,B]から一様乱数で決定します。ここで、
A = min(a,b) - αd
B = max(a,b) + αd
d = |a - b|
αはパラメータ
です。
- UNDX
この交叉法は、次のように子を決めます。
- 2つの親個体をa,bとします。
- 親の中点を m = (a + b) / 2, 差ベクトルを d = (a - b)とします。
- 子個体cを以下の式に従って生成します。
c = m + ξd
ξ〜N(0,σ^2)
ここで、N(0,σ^2)は平均0、分散σ^2の正規分布を表しています。
シミュレータでは、標準偏差(SD)としてパラメータの設定を行います。SDの経験的な推奨値は0.5とされています。
RealGA Mutation
この項目は、Real GAのときのみ作用します。
- Uniform distribution
一様乱数によって突然変異を起こします。手順は次の通りです。ここで、xの範囲を[X_MIN,X_MAX]とし、親個体をxとします。
- 方向(正か負か)を1/2の確率で選びます。
- 正のとき、[x,min(x+M,X_MAX)]から一様ランダムに選びます。
- 負のとき、[min(X_MIN,x-M),x]から一様ランダムに選びます。
- Normal distribution
正規分布によって突然変異を起こします。このとき用いる正規分布は親個体をxすると、平均x、分散SD^2です。xの範囲を超えて生成された個体は、範囲内に収められます。
Result
- Generation,Evaluation Time
ここに表示されるのはGAのときは世代数、山登り法のときは評価回数です。
- Maximum(X,Y)
ここでは各世代での最高値のX座標とY座標を表示します。赤丸が表示されているところです。
適合度グラフ
- generation, fitness
各世代の適合度をグラフ化しています。山登り法を比較できるように、「世代数×個体数」が評価回数と一致するようになっています。つまり、山登り法を行う場合、「評価回数/個体数」がgenarationとして表示されています。
- best, average
各世代での最高の適合度と、平均の適合度をグラフ化しています。
- グラフのコピー
グラフを右クリックすると、コピーできるようになっています。このとき、ビットマップ形式とメタファイル形式(EMF形式)が選べるようになっています。レポート作成時などにご利用下さい。
