締め切り

第一回レポート（第1問～第6問）：12月18日の２３：５９まで。

第二回レポート（第7問～第12問）：2月4日の２３：５９まで。

注意事項

• 講義の内容により変更の可能性がある。最終的な内容は必ず講義の際に確認すること。
• 各回で提出する課題数は任意であるが、最低数は1問である。 問題の難易度を印で示しているので、提出の際の参考にすること。 簡単な問題であれば2問以上を提出することがのぞましい。
• 原則として、締切日より遅れて提出された場合は 採点の対象としない。 ただし、何らかの理由があれば、 締め切りまでに提出したレポートについて更新・修正版をのちに 提出することは認めることがある。
• また、特段の理由があれば提出期限を延長する。
• 東大サーバーの不調などにより、提出用サイトにアクセスできないことがあるようです。そのため余裕をもって提出してください。締め切り直前にその事象が発生した場合にはITC-LMSに提出してください。

レポート採点方針

• 当然ながら提出したからといって満点とは限らない。
• とりあえず適当に書いて提出するというのは印象が悪いので注意せよ。
• 最終評価は合計点をもとにした相対評価となる。
• 難しい問題に挑戦したり、多くの人が解かないような問題を解答すると ポイントが高い。
• ＡＩらしいユニークな解答も評価する。
• 参考までに★で難易度を示しておく。

課題内容

1. （第1問：課題番号01★） 強いAI (汎用AI)の実現可能性（すでにAIはできている？）と、それに関する脅威について論ぜよ。とくに、LLM(大規模言語モデル)は意識を持てるか、自分が機械やLLMであるとはどういうことか、について自分の経験などを通して考察すること。

   A4で５～７ページ程度とする。 少なすぎるもの・内容がないものは採点しない。

   以下のコンテンツを2つ以上参照すること。

   • コウモリであるとはどのようなことであろうか？（「ダグラス・R. ホフスタッター, D.C. デネット:"マインズ・アイ―コン ピュータ時代の「心」と「私」", 阪急コミュニケーションズの第２４章」）
   • 瀬名秀明:"デカルトの密室",新潮社
   • 未来の二つの顔, ジェイムズ・Ｐ・ホーガン
   • ロジャー・ペンローズ:"皇帝の新しい心―コンピュータ・心・物理法則", みすず書房
   • 超人類（ポストヒューマン）
     • 「トランス・ヒューマニスト」協会, 知性強化製品
     • ニック・ボストロム:"スーパーインテリジェンス 超絶AIと人類の命運",日本経済新聞出版社
   • シミュレーション仮説
     • ニック・ボストロム(オックスフォード大学の哲学者)は、我々が 実は人間ではなく、他の人々（？）に作られた超高性能コンピュータ上でのシミュレーションと本気で論じている。人類が、宇宙人が作ったスーパーコンピュータの中のシミュレーション世界にすむ仮想的な存在であるという仮説を否定できないことを証明した。
     • ARE YOU LIVING IN A COMPUTER SIMULATION? BY NICK BOSTROM [Published in Philosophical Quarterly (2003) Vol. 53, No. 211, pp. 243‐255. (First version: 2001)]
   • ベンジャミン・リベット(アメリカの生理学者)による 準備電位の実験 では、 「手を動かす」という意識（思ったとき）よりも、そのための準備電位が先行することが分かった。つまり神経生理学は自由意志の存在を証明できない。したがって、 人間には自由意志が存在しない。
   • 色彩ファイ現象: 2つの異なる色によるファイ現象では、中間点で突然に色が変わるように観える。 なぜまだ第２の点が現れていないのに、途中に一点を記入・補填できるのか？ 脳は「予知」を無意識のうちにしているのか？
     • colored phi phenomena
     • 実験可能なアプレット
   • タコは痛みを感じるか、意識があるのか？
     • イギリスにはタコへの虐待を禁止する法律がある。
     • ただしオクトパス・ウルガリスのみで他の頭足類は含まれない。
     • 1986年制定：「名誉脊椎動物」とする。
     • 魚は傷みを感じるか？（ヴィクトリア・ブレイスウェイト，紀伊國屋書店）
   • ダニエル・デネット：「心はどこにあるのか？」「解明される意識」
   
   レポート提出のための注意事項
   1. レポートには以下の項目を含めること。
      1. 上のコンテンツの要約、主題、主旨。
      2. 考察および感想。 特に授業内容と 関連付けて考察するとポイントが高い。
      3. 疑問に思った点、理解しがたい点などの質問事項。
   2. LLMに聞いてみた、というのもアリだが、その経験内容を自分の言葉で述べること。
   3. 参照した文献、引用、出典は必ず文献リストに挙げること。
   
   
   
2. （第2問：課題番号02★）
講義で説明したように、 三段論法推論にはヒトにとって解きやすいものと解きにくいものがある。これについては、 メンタルモデル（ 教科書1.3節）による説明が認知科学的になされている。



（１）被験者に対して４つの三段論法に対して結論の真偽を尋ねたデータがここにある。データを適宜集計して正答率(もしくは部分的正解率)を表示せよ。

（２）LLM(大規模言語モデル)でも 三段論法が解けるらしい。実際に解かせてみよう。Chain of Thoughtや呪文を工夫してみよ。

（３）これらをふまえて、ヒトの知能とLLMとの類似性・違いを考察せよ。 また今後「強いAI」を実現するために、どのようなデータを集めて研究すべきか、論理的推論の必要性などについて論述せよ。参照した文献、引用文献、出典は必ず文献リストに挙げること。


Hint1: 三段論法推論を解くメンタルモデルのデモプログラムが以下にあるので必要なら利用しても良い。
• LISPによるプログラム
• pythonによるプログラムとその使い方
Hint2: 参考書 の『4.4節：三段論法推論：ソクラテスは死ぬか？』では三段論法のメンタルモデルの詳細が説明されている。


3. （第3問：課題番号03★）次の2問にすべて答えること。
1. 進化計算の原理を身近な例を用いて分かりやすく説明せよ。少なくとも以 下の項目についてアナロジーで解説すること。
• 交叉
• 突然変異
• 世代交代
• 集団初期化
• 選択・淘汰
• 適合度計算
• 探索が上手くいくようす
図と例証を用いて示すと良い。 講義では、飛行機、鉄道、動物などの例を用いた。 オリジナルでないものは採点しない。
2. 進化計算の面白い応用例・実用例について調べて考察せよ。

講義などで説明した例や以下のような著名な例は除く。

• 遺伝的アルゴリズムでブランコの漕ぎ方を学習させた動画
• 進化するマリオのお話
• 対話型似顔絵作成システムNIGAO
• グラディウスを学習させてみた
• 機械学習する物理エンジンの豚
• 自転車の形状と車輪の進化的設計
• 2013年Yahoo! が買収したSummly（メールやブログの内容を自動で要約するGAに基づくアルゴリズム）
• GAでモナリザを描く
• Mondriaan Art by Evolution on the Web
• オノマトペ自動生成システム
• 電車広告
• 遺伝的アルゴリズムを用いてハイハイを学習させる
• 顔モルフ
• 畝見先生のSBART(抽象画生成)
• Autodesk社がAirbus社と共同で航空機のキャビン内で使用するパーティションの設計に 進化計算を利用した
• Synplant「遺伝を利用したソフトウェアシンセサイザ」
• 漢詩生成
• 『グリムノーツRepage』から見る遺伝的アルゴリズムのゲームバランス調整における事例とその可視化
• 進化計算DARWIN｜オープンハウスの宅地自動区割りに活用
• 物流センター在庫配置最適化

なおこの課題で求めているのはわかりやすいデモや応用であり、 学術論文や技術的詳細ではない。

実応用例については、 特許・新聞記事・論文などの出典とともに、どのように応用されているかをわかりやすく平易な言葉で説明すること。




4. （第4問：課題番号04★★）
川を渡るパズル(教科書の例題3.1）の以下ような拡張を考えよう。講義では、宣教師と人食い人間のパズルの解法について説明した。
N組の夫婦がこちらの岸にいて、二人乗りのボートを使って川を渡りたい。夫はとても嫉妬深く、自分がその場にいなければ妻がほかの男と同じところにいることを許さない。


（１）N=3について解を探索せよ。 A*,深さ優先,広さ優先探索をそれぞれ実行して探索の効率（解に到達するまでのノー ドの展開数）を比較すること。

（２）Nが4のときには解がないことが知られている（これを示せるか？）。ところが、川の真ん中に島があると解くことができるらしい。 この場合の解を探索せよ。ただし一方の岸から反対岸に直接ボートを進めることはできない。 A*のヒューリスティックスを複数考えて探索効率（解に到達するまでのノー ドの展開数）を比較すること。

（３） 上の問題について、一方の岸から反対岸に直接ボートを進めることが出来る場合には解があるだろうか？

（４） 余裕があれば、Nが5以上の場合にどのようになるのかを考察せよ。これは必ずしも解く必要はない。

講義で説明した以下のプログラムを拡張するとよい。
• 8パズル（深さ優先探索）
• 8パズル（広さ優先探索）
• 8パズル（Ａ＊探索）

自分でA*用の（効果的な）ヒューリスティックスを考えて実験してみよう。



5. （第5問：課題番号05★★）
GAの探索問題として適当な例題を考えよ(TSPとNクィーン問題はのぞく)。
もし何もアイディアがないなら、 AtCoder上の『競技プログラミングの鉄則　演習問題集』のA47-50かB46-49のどれか１問を選ぶこと。A49が一番お奨めである。A46はTSPなので除く。
このとき、その問題に関して次の３つの異なったGAの性能を比較しなさい。
• 標準的なGA（ダーウィン進化）
• ボールドウィン進化 型GA：個体の適合度を評価するため、その個体をスタート地点としてとり、局所解に達するまで山登り法などで局所探索を実施する。もとの個体の適合度は上で得られた局所最適解である。しかし子孫を作るときには、局所探索による「学習済み」の改善個体ではなく、オリジナルの個体の遺伝子型が用いられる。
• ラマルク進化型GA：ボールドウィン進化と同じく、局所探索を行い適合度を評価する。 ただし、局所探索で改良された個体によって子孫が作られる。つまり獲得形質を受け継ぐ。





これら３つのGAについて、得られた解の品質と解を見つけるまでにかかった時間(必要な世代数、計算時間)について 比較せよ。 簡単な問題から難しいさまざまな問題に対して実験するとよい。
Hint1: AtCoderの課題提出を求めているのではない。そのため課題条件を適宜変更してかまわない。例えば、解を見つけるでの実行時間を比較ではなく、進化において何世代で解が見つかったかを比較するとよい。
Hint2: ボールドウィン進化とラマルク進化の詳細は 参考書 の5.1節にある。


6. （第6問：課題番号06★★★）
平面上に23個の点をできるだけ「美しく」配置せよ。
23という数の個性をどのように生かして探索したのかについて説明すること。
見やすくなるために必要なら補助線（曲線）を書き加えよ。

• 例えば、10個の点であれば以下のようなものが考えられる。

  

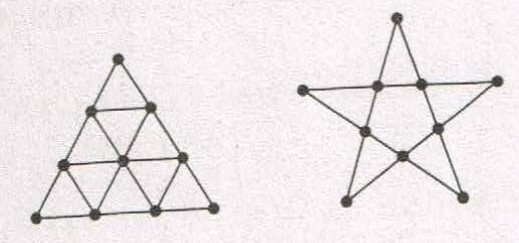
• 進化計算を推奨するが、ニューラルネット、強化学習、その他のAI手法で探索してもよい。
• 評価関数（「美しさ」の基準、適合度）を工夫すること。例えば、対称性の個数、直線状に並んだ数、思いつきにくさ、希少性、力学的エネルギ―最小化などが考えられる。
• 個性を生かすことが重要なので、他の点数でも配置可能なもの（円周上、直線上など）はポイントが低い。
• 必ずしも最適解(?)が得られなくても成績評価には関係しない。 どれだけ工夫したか、考察したかで評価する。
• AI探索が目的なので、LLMに聞いたというような解答は原則的に認められない。

---

7. （第7問：課題番号07★） ヒトは確率推論が必ずしも得意ではない。またランダム性の認識に関しても間違えやすい。これらのことから、 スティーブン・ピンカー は「人間は合理性に反して、ある事象に明確な原因があると断定することがある」と述べている。では、LLM(や生成AI)とヒトはどのように違うのだろうか。これについて、自分の経験や検証実験などを通して考察せよ。
   少なすぎるもの・内容がないものは採点しない。
   以下のような手順をとること。
   

   （１）LLM(や生成AI)でいくつかの確率的推論を試す。promptや呪文、CoTなどさまざまに工夫してみて、答え方の違いや錯覚（hallucination）に注目すること。自分で工夫した例・考えた例などがあるとなお良い。

   （２）ヒトについての生データが以下にある。これらのいくつかを集計・整理する。すべてのデータを利用することはない。各自で取捨選択して回答すること。ヒトのコメントの錯覚部分が重要かもしれない。

   • 山田さん夫妻のこども
   • ヒカリムシとランダム点列
   • 落雷確率
   • 株価

   （３）以上をもとにして、LLM(や生成AI)とヒトにおける確率推論の類似性・相違点について考察せよ。 とくに、 スティーブン・ピンカー や ダニエル・デネット らの批判（「ベイズ推定や確率モデルをもとにした機械学習や深層学習では強いAIは造れない」）について思うところ（反論もしくは賛同など）を述べよ。

   （４）このような実験に関して今後工夫すべき点について考察せよ。例えば、LLMにどのような質問をすればよいか、ヒトに対してどのようなアンケートを集めるべきか、など。
   
   Hint1: ランダム性の錯誤（星座・ヒカリムシとランダムドット）、ギャンブラーの誤謬、ロンドンの爆撃については 参考書 の3.2節に説明されている。
   
   Hint2: 参考書 の2章、3章にある以下のような問題を利用すると良い。このうちの一部についてはアンケートや講義で説明している。当然ながら有名な問題をそのまま利用すると、解答例がLLMにあるので注意すること。
   

   • 乳がんの危険性
   • 山田さん夫妻のこども
   • 落雷の確率
   • ３囚人の問題
   • モンティホール問題
   • Truel

8. （第8回問：課題番号08★） 次の3問にすべて答えること。
   1. じゃんけんのゲームを行う サイト がある。 ほとんどの人は20回を超えると勝つことができない。 このAIは単にランダムに手を出しているのではない。
      なお、上のサイトが動かない場合には ここを試すこと。また、サイトの圧縮版が ここにある。
      何回かこのジャンケンAIと対戦してみて、その対戦結果を報告せよ。 自分が考える賢い戦略をいくつか試してみること。
   2. このジャンケンAIを作るのにどのような戦略を使えるのかを 解説せよ。 ただし「ナッシュ均衡解」や 「パレート効率性」という用語を必ず使用して説明すること。
   3. ポーカーの テキサス・ホールデム（Texas hold'em）は解かれたとされている。 この戦略について分かりやすく説明せよ。 この論文 を参考にするとよい。 ただし 「ナッシュ均衡解」やCFR(Counterfactual Regret Minimization)という用語を使用すること。

      

   Hint1: 人間はジャンケンをするときに ある行動パターンに従うことを発見した論文が ここ にある。
   Hint2: 上のジャンケンAIは 20万回以上のジャンケンで得られた知識に基づいているらしい。 そのデータを集めるサイトは ここ にある(Prof. Shawn Bayernによる)。これを基にしたジャンケンAIの サンプルプログラムは ここ にある。
   Hint3: AIに対戦する場合には参考にならないだろうが、 ヒトどうしのジャンケンで勝率を挙げる方法は提案されている。たとえば 「すイエんサー 目指せ！勝率８割　究極のじゃんけん必勝法を見つけた～い！」 にあるものなど。

9. （第9回問：課題番号09★） 講義では人間のリスク認知の偏りやヒューリスティックスとしてのプロスペクト理論について説明した。 では、LLM(や生成AI)も同じような認知や知覚の偏りを示すのであろうか？ 実験的に検証してみよう。
   少なすぎるもの・内容がないものは採点しない。
   以下のような手順をとること。
   

   （１）講義で説明したような質問をLLM(や生成AI)に対して行う。promptや呪文、CoTなどさまざまに工夫してみて、答え方の違いを観察すること。とくに、フレーミング効果、授かり効果、損失回避、Rabinの定理、アレのパラドクスなどに関する検証をする。すべてを対象にする必要はない。以降の問題に関して面白そうな題材をいくつか選択すること。自分で工夫した例・考えた例などがあるとなお良い。

   （２）ヒトのデータと比較して、ヒトとLLM(や生成AI)との認知の相違点・類似性について考察せよ。 これらをふまえて、LLMを実世界（金融やマーケットなど）に応用するときの課題・問題点を考慮すると良い。

   （３）このような実験に関して今後工夫すべき点について考察せよ。例えば、LLMにどのような質問をすればよいか、ヒトに対してどのようなアンケートを集めるべきか、など。
   
   Hint1: 講義資料は ここ にある。プロスペクト理論については 参考書 の６章に説明されている。
   
   Hint2: ヒトに対するデータは、上の講義資料に書かれている。また関連するアンケートデータは以下にある。適宜集計して使用してほしい。

   • 新聞購読のおとり広告
   • ラビンの定理
   
   Hint3: GPTにプロスペクト理論が適応するかについて調べた研究論文が ここにある。また、プロスペクト理論を想定して、金融やマーケットにLLMを利用する研究は ここにある。

10. （第10問：課題番号10★★） メタヒューリスティクスには、数多くの手法が 提案されている。たとえば以下のようなものがある。これらのいくつかは講義で説明した。
    • Artifical Bee Colny (ABC)
    • Ant colony optimization (ACO)
    • Particle Swarm Optimization (PSO)
    • カッコウ探索：Cuckoo search　
    • Harmony Search (HS)
    • カエル探索：Shuffled Frog-Leaping Algorithm (SFLA)
    • Honey-Bee Mating Optimization (HBMO)
    • Invasive Weed Optimization (IWO)
    • Teaching-Learning-Based Optimization (TLBO)
    • ホタル探索：Firefly Algorithm (FA)
    • コウモリ探索：Bat Algorithm (BA)
    • Plant Propagation Algorithm (PPA)
    • Water Cycle Algorithm (WCA)
    • Symbiotic Organisms Search (SOS) algorithm
    • Harris hawks optimization (HHO)
    • Black Hole Algorithm (BHA)
    • Fruit fly optimization algorithm (FOA)
    • Ant lion optimizer (ALO)
    • Moth-flame optimization algorithm (MFO)
    • Elephant herding optimization (EHO)
    • Coral reef optimization
    • Monarch butterfly optimization
    • Egyptian Vulture Optimization
    • Lion swarm optimization
    • ネコ探索：Cat swarm optimization
    • ゴキブリ探索：Cockroach Swarm Optimization
    • バクテリア探索：Bacterial Foraging Optimization
    • 灰色オオカミ探索：Grey Wolf Optimiation (GWO)
    • 花火アルゴリズム：fireworks algorithm
    • クジラ探索：Whale optimization algorithm
    • リス探索：Squirrel search algorithm
    • 重力探索：Gravitational search algorithm (GSA)
    • ひらめき探索：Brain Storm Optimization (BSO)
    • 集団心理療法探索：Group Counseling Optimization (GCO)

    

    
    なお、メタヒューリスティックス研究に関しては、玉石混交であったり、同じような手法の重複提案であるような批判もなされている。その詳細は 『深層学習とメタヒューリスティクス ディープ・ニューラルエボリューション（6.8節）』 にある。
    ここでは、LLM(や生成AI)に基づいて新しいメタヒューリスティックを提案し、実際にコード化をして動作確認をしてみよう。 以下の手順にしたがうこと。
    

    （１）LLMにメタヒューリスティックスの例を３～６個程度あげさせて、その詳細について説明してもらう。特定のキーワードをpromptに入れた方がよい。例：大域的探索のため、群知能、組み合わせ探索、など。

    （２）（１）であげられたそれぞれのアルゴリズムに関して、重要な特徴や探索性能に影響を与える要素に関して説明させる。それの妥当性について考察せよ。幻覚症状（hallucination）に注意すること。

    （３）特定のタスクに対して、（１）であげられたメタヒューリスティックスのハイブリッド版やそれらの改良版を提案させる。それについて説明させ、pseudo-codeやpython codeを出力させる。特定タスクとしては、TSPやNクィーンのような具体的な問題などでよいが、有名な問題には解答例がLLMにあるので面白くない。より一般的な探索問題として指定することを奨励する。
    Hint: promptとしては、「多様性を維持せよ」、「exploration(探査)とexploitation(利用)の効果的なバランスをとれ」、「局所解に陥らない」、「目的関数の評価回数をできるだけ少なくする」など講義で説明した探索に重要な要素を入れるのが好ましい。

    （４）実際にpseudo-codeを実行させてLLMの提案を検証する。（３）で想定したタスクを実際に解かせてみる。その上で、fatal　error（明確なバグ）があるか・修正可能か、実行レベルでの性能、計算効率、すでにあるメタヒューリスティックスとの比較、などについて考察せよ。

    なお、ここではLLMを利用してメタヒューリスティックスのハイブリッド法や新手法を提案することを目指しているので、得られたメタヒューリスティックスが不十分であっても問題ない。むしろ、LLMを利用する場合の有用性や欠点、拡張点を考察してほしい。

    
    Hint1: メタヒューリスティックスについて、最近の解説には以下のような論文がある。
    1. Crow Search Algorithm: Theory, Recent Advances, and Applications
    2. Sea Lion Optimization Algorithm for Solving the Maximum Flow Problem
    
    Hint2: LLMでメタヒューリスティックスのアルゴリズムを創る論文は ここ にある。

11. （第11問：課題番号11★★★） 講義ではアリのフェロモンによる効率的な探索について説明した。 しかしながらこれは一面であり、それほど簡単ではないことが知られている。 例えば、人工生命としては以下のような拡張が面白い。
    
    • アリはそれほど勤勉ではなくサボるのがいる。働き始める閾値が違う。その研究はここにある。以下のようにするとよい。
      1. アリの数を限定する。各アリの働き始める閾値をランダムに決める。
      2. 閾値の低いアリから餌集めに従事する。
      3. 餌集めの効率が下がると閾値の高いアリが餌集めをし始める。
    • アリは複数のフェロモンを利用するらしい（揮発度も異なるらしい）を落とす。その研究はここにある。以下のようにするとよい。
      1. ランダム探索時と帰巣時には別のフェロモンを落とす。
      2. 2つのフェロモンの揮発度が異なる。探索フェロモンの方が早く蒸発する。
      3. 探索フェロモンを忌避する傾向がある（ネガティブ・フェロモン）。
    
    では、このいずれかに関してシミュレーションで検証してみよう。 できれば頑強性(餌の数や位置への変化、障害物の出現、部分的なアリの消滅などへの頑強性)を比較すると良い。ただし、必ずしも的確に比較できなくても成績評価には関係しない。 どれだけ工夫したか、考察したかで評価する。
    
    Hint: アリのフェロモン・トレイルのシミュレーションプログラムは以下で提供している。 その他にもいろいろとあるので、各自の得意な環境を探すとよい。
    1. アリの知恵（6.1節）
    2. Ant Simulation by Python
    3. Swarmの教科書の9.7節。上のシミュレーションのJava版コード。Swarmのインストールが必要なので、アルゴリズムを参考にする程度が望ましい。

12. （第12問：課題番号12★★★） メタヒューリスティックスを用いた多目的最適化のシミュレータを作成せよ。 2次元のパレートフロントをうまくとらえられるかを実験してみよう。

    以下のいずれかの手法を１つ以上(できれば２つ)用いること。

    • ACO (Ant colony optimization)
    • See Lion algorithm
    • Whale Optimization Algorithm
    • CS (cuckoo search)

    講義で説明した多目的最適化のVEGAシミュレータは ここにある（java executable file）。 またシミュレータの使用方法はここにある。 javaソースファイルははここにある。

    以下に述べられている例題か自分で考えた面白い例題を試すこと。 パレートフロントが異なる問題（凸型フロント、凹型フロントなど）の実験を行って 結果を観察するとよい。

    • 多目的最適化例題集
    • 多目的最適化の分かりやすい説明と例題のある論文

    探索で得られたパレート解の 精度に対する評価指標としては以下の2つを用いるとよい。

    • 優越個体割合（Ratio of Non-dominated Individuals: RNI）
    • 解の多様性の評価指標として被覆率（Cover Rate: CR）詳しくはこの資料を参照。
    
    Hint1: VEGAのアルゴリズムとシミュレータの解説は この本の5.6節にある。
    Hint2: 以下の論文などが参考になる。
    • 多目的ACO
    • 多目的See lion
    • 多目的 whale optimization
    • 多目的CS

提出方法

以下のものを提出すること。提出方法はここに示す通りである。

• プログラムを作成した場合、 実現したシステムに関する説明（どの部分をどう創意工夫したかなど）。さら にアルゴリズム、ソースリストの説明。
• 結果の表示（グラフなどを用いると分かりやすい）。
• 結果に関する考察と評価。
• 授業に関するコメント、要望など（次回の参考にするので是非書いて下さい）。